Target Population, Access Frame, and Sample
2.2. Target Population, Access Frame, and Sample#
An important initial step in the data lifecycle is to express the question of interest in the context of the subject area and consider the connection between the question and the data collected to answer that question. It’s a good practice to do this before even thinking about the analysis or modeling steps because it may uncover a disconnect where the question of interest cannot be directly addressed by the data. As part of making the connection between the data collection process and the topic of investigation, we identify the population, the means to access the population, instruments of measurement, and additional protocols used in the collection process. These concepts—the target population, the access frame, and the sample—help us understand the scope of the data, whether we aim to gain knowledge about a population, scientific quantity, physical model, social behavior, or something else.
- Target population
The target population consists of the collection of elements comprising the population that you ultimately intend to describe and draw conclusions about. The element may be a person in a group of people, a voter in an election, a tweet from a collection of tweets, or a county in a state. We sometimes call an element a unit or an atom.
- Access frame
The access frame is the collection of elements that are accessible to you for measurement and observation. These are the units through which you can study the target population. Ideally, the access frame and population are perfectly aligned; meaning they consist of the exact same elements. However, the units in an access frame may be only a subset of the target population; additionally, the frame may include units that don’t belong to the population. For example, to find out how a voter intends to vote in an election, you might call people by phone. Someone you call may not be a voter, so they are in your frame but not in the population. On the other hand, a voter who never answers a call from an unknown number can’t be reached, so they are in the population but not in your frame.
- Sample
The sample is the subset of units taken from the access frame to observe and measure. The sample gives you the data to analyze in order to make predictions or generalizations about the population of interest. When resources have been put into following up with nonrespondents and tracking down hard-to-find units, a small sample can be more effective than a large sample or an attempt at a census where subsets of the population have been overlooked.
The contents of the access frame, in comparison to the target population, and the method used to select units from the frame to be in the sample are important factors in determining whether or not the data can be considered representative of the target population. If the access frame is not representative of the target population, then the data from the sample is most likely not representative either. And if the units are sampled in a biased manner, problems with representativeness also arise.
You will also want to consider time and place in the data scope. For example, the effectiveness of a drug trial tested in one part of the world where a disease is raging might not compare as favorably with a trial in a different part of the world where background infection rates are lower (see Chapter 3). Additionally, data collected for the purpose of studying changes over time, like with the monthly measurements of carbon dioxide (CO2) in the atmosphere (see Chapter 9) and the weekly reporting of Google searches for predicting flu trends have a temporal structure that we need to be mindful of as we examine the data. At other times, there might be spatial patterns in the data. For example, the environmental health data, described later in this section, are reported for each census tract in the state of California, and we might make maps to look for spatial correlations.
And if you didn’t collect the data, you will want to consider who did and for what purpose. This is especially relevant now since more data is passively collected instead of collected with a specific goal in mind. Taking a hard look at found data and asking yourself whether and how these data might be used to address your question can save you from making a fruitless analysis or drawing inappropriate conclusions.
For each of the following examples, we begin with a general question, narrow it to one that can be answered with data, and in doing so, identify the target population, access frame, and sample. These concepts are represented by circles and rectangles in diagrams, and the configuration of the overlap of these shapes helps reveal key aspects of the scope. Also in each example, we describe relevant temporal and spatial features of the data scope.
What makes members of an online community active? Content on Wikipedia is written and edited by volunteers who belong to the Wikipedia community. This online community is crucial to the success and vitality of Wikipedia. In trying to understand how to incentivize members of online communities, researchers carried out an experiment with Wikipedia contributors as subjects. A narrowed version of the general question asks: do awards increase the activity of Wikipedia contributors? For this experiment, the target population is the collection of top, active contributors—the 1% most active contributors to Wikipedia in the month before the start of the study. The access frame eliminated anyone in the population who had received an incentive (award) that month. The access frame purposely excluded some of the contributors in the population because the researchers wanted to measure the impact of an incentive, and those who had already received one incentive might behave differently (see Figure 2.1).
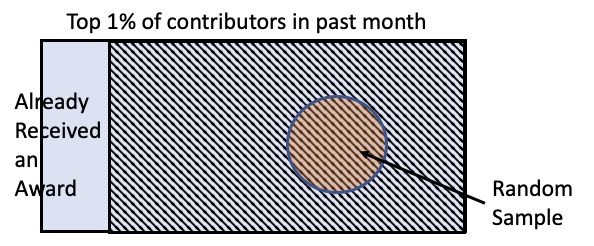
Fig. 2.1 Representation of scope in the Wikipedia experiment#
The sample is a randomly selected set of 200 contributors from the frame. The sample of contributors were observed for 90 days, and digital traces of their activities on Wikipedia were collected. Notice that the contributor population is not static; there is regular turnover. In the month prior to the start of the study, more than 144,000 volunteers produced content for Wikipedia. Selecting top contributors from among this group limits the generalizability of the findings, but given the size of the group of top contributors, if they can be influenced by an informal reward to maintain or increase their contributions, this is still a valuable finding.
In many experiments and studies, we don’t have the ability to include all population units in the frame. It is often the case that the access frame consists of volunteers who are willing to join the study/experiment.
Who will win the election? The outcome of the US presidential election in 2016 took many people and many pollsters by surprise. Most pre-election polls predicted Clinton would beat Trump. Political polling is a type of public opinion survey held prior to an election that attempts to gauge whom people will vote for. Since opinions change over time, the focus is reduced to a “horse-race” question, where respondents are asked whom they would vote for in a head-to-head race if the election were tomorrow: Candidate A or Candidate B.
Polls are conducted regularly throughout the presidential campaign, and as election day approaches, we expect the polls to get better at predicting the outcome as preferences stabilize. Polls are also typically conducted statewide and later combined to make predictions for the overall winner. For these reasons, the timing and location of a poll matters. The pollster matters too; some have consistently been closer to the mark than others.
In these pre-election surveys, the target population consists of those who will vote in the election, which in this example was the 2016 US presidential election. However, pollsters can only guess at whether someone will vote in the election, so the access frame consists of those deemed to be likely voters (this is usually based on past voting records, but other factors may also be used to determine likely voters). And since people are contacted by phone, the access frame is limited to those who have a landline or mobile phone. The sample consists of those people in the frame who are chosen according to a random dialing scheme (see Figure 2.2).
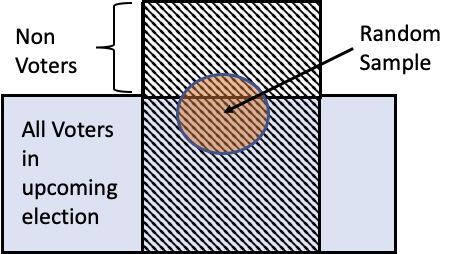
Fig. 2.2 Representation of scope in the 2016 presidential election survey#
In Chapter 3, we discuss the impact on the election predictions of people’s unwillingness to answer their phone or participate in the poll.
How do environmental hazards relate to an individual’s health? To address this question, the California Environmental Protection Agency (CalEPA), the California Office of Environmental Health Hazard Assessment (OEHHA), and the public developed the CalEnviroScreen project. The project studies connections between population health and environmental pollution in California communities using data collected from several sources that include demographic summaries from the US census, health statistics from the California Office of Statewide Health Planning and Development (now known as the California Department of Health Care Access and Information), and pollution measurements from air monitoring stations around the state maintained by the California Air Resources Board.
Ideally, we want to study the people of California and assess the impact of these environmental hazards on an individual’s health. However, in this situation, the data can only be obtained at the level of a census tract. The access frame consists of groups of residents living in the same census tract. So the units in the frame are census tracts and the sample is a census—all of the tracts—since data are provided for all of the tracts in the state (see Figure 2.3).
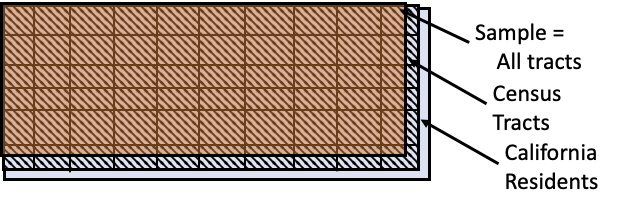
Fig. 2.3 Scope of the CalEnviroScreen project; the grid in the access frame represents the census tracts#
Unfortunately, we cannot disaggregate the information in a tract to examine an individual person. This aggregation impacts the question we can address and the conclusions that we can draw. For example, we can ask questions about the relation between rates of hospitalizations due to asthma and air quality in California communities. But we can’t answer the original question posed about an individual’s health.
These examples have demonstrated possible configurations for a target, access frame, and sample. When a frame doesn’t reach everyone, we should consider how this missing information might impact our findings. Similarly, we ask what might happen when a frame includes those not in the population. Additionally, the techniques for drawing the sample can affect how representative the sample is of the population. When you think about generalizing your data findings, you also want to consider the quality of the instruments and procedures used to collect the data. If your sample is a census that matches your target, but the information is poorly collected, then your findings will be of little value. This is the topic of the next section.
