What to Look For in a Distribution
10.2. What to Look For in a Distribution#
Visual displays of a feature can help us see patterns in observations; they are often much better than direct examination of the numbers or strings themselves. The simple rug plot locates each observation as a “yarn” in a “rug” along an axis. The rug plot can be useful when we have a handful of observations, but it soon gets difficult to distinguish high-density (most populated) regions with, say, even 100 values. The following figure shows a rug plot with about 150 longevity values for dog breeds along the top of a histogram:
px.histogram(dogs, x="longevity", marginal="rug", nbins=20,
histnorm='percent', width=350, height=250,
labels={'longevity':'Typical lifespan (yr)'},
)
Although we can see an unusually large value that’s greater than 16 in the rug plot, it’s hard to compare the density of yarns in the other regions. Instead, the histogram gives a much better sense of the density of observations for various longevity values. Similarly, the density curve shown in the following figure gives a picture of the regions of high and low density:
from scipy.stats import gaussian_kde
new_x = dogs['longevity'].dropna()
bandwidth = 0.2
xs = np.linspace(min(new_x), max(new_x), 100)
ys = gaussian_kde(new_x, bandwidth)(xs)
f2 = go.Figure(go.Scatter(x=xs, y=ys))
f2.update_xaxes(range=[4.5, 18.5], title="Typical lifespan (yr)")
f2.update_layout(showlegend=False,width=350, height=250)
f2.show()
In both the histogram and density curve, we can see that the distribution of longevity is asymmetric. There is one main mode around 12 years and a shoulder in the 9–11-year range, meaning that while 12 is the most common longevity, many breeds have a longevity one to three years shorter than 12. We also see a small secondary mode around 7, and a few breeds with longevity as long as 14 to 16 years.
When interpreting a histogram or density curve, we examine the symmetry and skewness of the distribution; the number, location, and size of high-frequency regions (modes); the length of tails (often in comparison to a bell-shaped curve); gaps where no values are observed; and unusually large or anomalous values. Figure 10.1 provides a characterization of a distribution with several of these features. When we read a distribution, we connect the features that we see in the plot to the quantity measured.
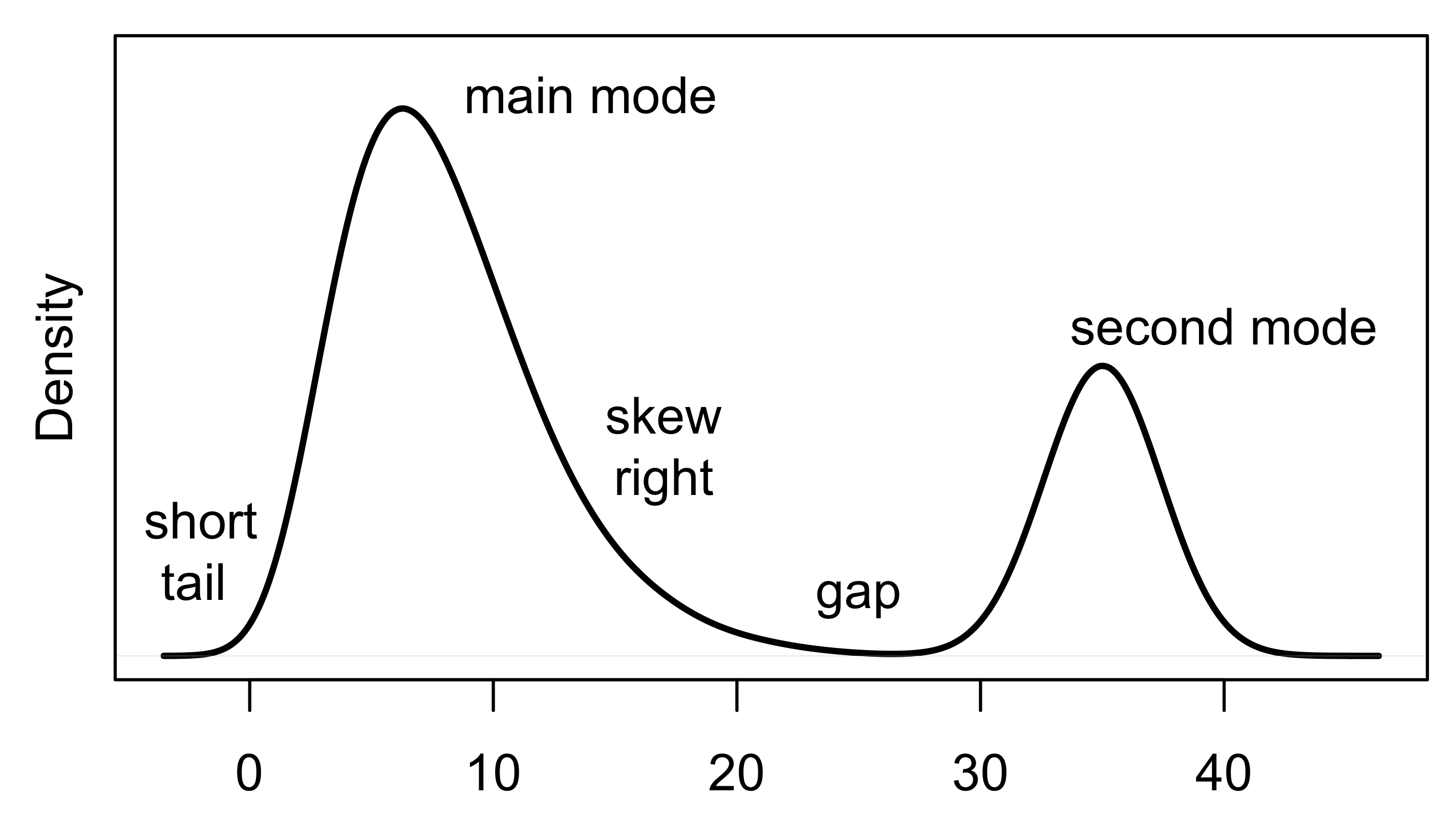
Fig. 10.1 Example density plot identifying qualities of a distribution based on its shape#
As another example, the distribution of the number of ailments in dog breed appears in the following histogram:
bins = [-0.5, 0.5, 1.5, 2.5, 3.5, 9.5]
g = sns.histplot(data=dogs, x="ailments", bins=bins, stat="density")
g.set(xlabel='Number of ailments', ylabel='density');
A value of 0 means this breed has no genetic ailments, 1 corresponds to one genetic ailment, and so on. From the histogram, we see that the distribution of ailments is unimodal with a peak at 0. We also see that the distribution is heavily skewed to the right, with a long right tail indicating that few breeds have between four and nine genetic ailments. Although quantitative, ailments is discrete because only a few integer values are possible. For this reason, we centered the bins on the integers so that the bin from 1.5 to 2.5 contains only those breeds with two ailments. We also made the rightmost bin wider. We lumped into one bin all of the breeds with four to nine ailments. When bin counts are small, we use wider bins to further smooth the distribution because we do not want to read too much into the fluctuations of small numbers. In this case, none of the breeds have six or seven ailments, but some have four, five, eight and nine.
Next, we point out three key aspects of histograms and density curves: the \(y\)-axis should be on a density scale; smoothing hides unimportant details; and histograms are fundamentally different from bar plots. We describe each in turn.
- Density in the y-axis
The y-axes in the histograms of longevity and ailments are both labeled “density.” This label implies that the total area of the bars in the histogram equals 1. To explain, we can think of the histogram as a skyline with tall buildings having denser populations, and we find the fraction of observations in any bin from the area of the rectangle. For example, the rectangle that runs from 3.5 to 9.5 in the ailments histogram contains about 10% of the breeds: 6 (width) × 0.017 (height) is roughly 0.10. If all of the bins are the same width, then the “skyline” will look the same whether the y-axis represents counts or density. But changing the y-axis to counts in this histogram would give a misleading picture of a very large rectangle in the right tail.
- Smoothing
With a histogram we hide the details of individual yarns in a rug plot in order to view the general features of the distribution. Smoothing refers to this process of replacing sets of points with rectangles; we choose not to show every single point in the dataset in order to reveal broader trends. We might want to smooth out these points because this is a sample and we believe that other values near the ones we observed are reasonable; and/or we want to focus on general structure rather than individual observations. Without the rug, we can’t tell where the points are in a bin. Smooth density curves, like the one we showed earlier for longevity, also have the property that the total area under the curve sums to 1. The density curve uses a smooth kernel function to spread out the individual yarns and is sometimes referred to as a kernel density estimate or KDE for short.
- Bar plot ≠ histogram
With qualitative data, the bar plot serves a similar role to the histogram. The bar plot gives a visual presentation of the “popularity” or frequency of different groups. However, we cannot interpret the shape of the bar plot in the same way as a histogram. Tails and symmetry do not make sense in this setting. Also, the frequency of a category is represented by the height of the bar, and the width carries no information. The two bar charts that follow display identical information about the number of breeds in a category; the only difference is in the width of the bars. In the extreme, the rightmost plot eliminates the bars entirely and represents each count by a single dot. (Without the connecting lines, this figure is called a dot plot.) Reading this line plot, we see that only a few breeds are unsuitable for children:
kid_counts = dogs.groupby(['kids']).count()
kid_counts = kid_counts.reindex(["high", "medium", "low"])
fig = make_subplots(rows=1, cols=3)
fig.add_trace(go.Bar(x=kid_counts.index, y=kid_counts['breed']), row=1, col=1)
fig.add_trace(go.Bar(x=kid_counts.index, y=kid_counts['breed']), row=1, col=2)
fig.update_traces(width=0.1, row=1, col=2)
fig.add_trace(go.Scatter(x=kid_counts.index, y=kid_counts['breed'],
mode='markers+lines'), row=1, col=3)
fig.update_xaxes(title='Breed suitable for kids', row=1, col=2)
fig.update_yaxes(title='count', row=1, col=1)
fig.update_yaxes(range=[0,70])
fig.update_layout(showlegend=False,width=650, height=250)
fig.show()
Now that we have covered how to examine distributions of single features, we turn to the situation when we want to look at two features and how they relate.
